武田塾 尾張旭校
武田塾尾張旭校の校舎雰囲気や教室風景




武田塾尾張旭校の基本情報
- 住所
- 〒488-0014
愛知県尾張旭市三郷町中井田41番地
井上ビル2F
- 受入学生
- 既卒生 高校3年生 高校2年生 高校1年生 中学生
- TEL
- 電話受付時間
-
水曜日13:30~22:00
その他の曜日・祝日はこちら木曜日13:30~22:00
金曜日13:30~22:00
土曜日13:30~22:00
日曜日休校
月曜日13:30~22:00
火曜日13:30~22:00
祝日13:30~22:00
- 自習室利用時間
-
水曜日13:30~22:00
その他の曜日・祝日はこちら木曜日13:30~22:00
金曜日13:30~22:00
土曜日13:30~22:00
日曜日休校
月曜日13:30~22:00
火曜日13:30~22:00
祝日13:30~22:00
- 最寄り駅
- 名鉄瀬戸線 三郷駅 徒歩2分
- 近隣エリア
- 長久手市、春日井市、多治見市、名古屋市守山区・千種区・名東区・北区、尾張旭市、豊田市、日進市
- 休校情報など
【6月の休校日のご案内】
皆さま平素より大変お世話になっております。
武田塾尾張旭校です
6月の休校日スケジュール
️6/23月曜日休校日
️6/12木曜日は15:00-22:00が営業時間です。
自習室も15:00-22:00
️6/14土曜日は13:30-18:00閉店
自習室も18:00に閉まります
特訓スケジュールにはご注意ください。 よろしくお願いします
60秒でわかる武田塾

お問い合わせ
武田塾尾張旭校の
校舎長あいさつ

岩田 校舎長
武田塾 尾張旭校 校舎長の岩田です。
【武田塾とはどんな塾か?】 武田塾を一言で説明すると、ズバリ「授業をしない塾!」です。 「授業をしないのなら、一体何をしに塾に行くの?」という疑問が出てくると思います。
これについて、簡単に説明させていただくと、武田塾は生徒の皆さんが実際に学力を上げることができるポイントは授業ではなく、もっと根本的な部分、すなわち「自学自習」であると考えております。
自学自習はしっかりとした正しい方法で継続して行えば、劇的に大きな効果を上げることができます。
しかし、自学自習すること自体をおろそかにするのは論外ですが、自分なりに一生懸命やっているつもりでもペースが遅すぎたり、勉強方法自体を間違えていたり、勉強のやり方がわからなかったり、反復回数などが足りていなかったりすると十分な効果を発揮することはできません。
武田塾はその学習において超重要ポイントを徹底的に管理しサポートしていきます。
「もっと武田塾について詳しく知りたい!」と少しでも興味をお持ちになられましたら、ご気軽にご連絡下さい!
無料受験相談では「効率的に点数をとるための正しい勉強方法」などをご紹介しております。
少しでも今の成績に不安があるなら、是非1度武田塾瀬戸校へご連絡いただければその不安を解決できると思います。
武田塾の合格実績
尾張旭校の合格体験記

尾張旭校の合格実績
国公立大学
- 🌸名古屋大学 理学部
- 🌸国際教養大学 教養学部
- 🌸名古屋市立大学 看護学部
- 🌸都留文科大学 文学部
- 🌸福井大学 工学部
- 🌸岐阜大学 応用生物学部
- 🌸名古屋大学
- 🌸東京外国語大学
私立大学
- 🌸中央大学 理学部
- 🌸学習院大学 文学部
- 🌸東洋大学 法学部
- 🌸南山大学 外国語学部
- 🌸愛知大学 法学部
- 🌸帝京大学 法学部
- 🌸中京大学 国際学部
- 🌸早稲田大学 人間科学部
- 🌸同志社大学 社会政策学部
- 🌸立命館大学 政策科学部
- 🌸立命館大学 食マネジメント学部
武田塾尾張旭校って
どんなことするの?
-

授業を受けた=成績が上がるは大間違いです。
武田塾では、授業を受けるという無駄な時間を廃止し、「やってみる」から「できる」の過程に重きを置いています。 -

参考書による自学自習なら、得意な科目はサクサク進められ、苦手な科目はじっくり丁寧に取り組めます。一人ひとりのペースに合った効率的な勉強法で、大学受験にしっかり向き合えます。
-

定期テストや中学・高校・大学受験で成果を出すには、日々の勉強で解けるまで繰り返し復習することが大切です。武田塾では、「4日進んで2日復習する」学習方法で、効率よく記憶を定着させることができます。
-

毎日やるべき課題を「宿題」として明確に「全指定」!
さらに、特訓の開始時に行う「テスト」でしっかり宿題をしているか確認。ここまでやる"超"個別指導だから短期間で実力がつくのです。
あなたに合った勉強法を教えます!
無料受験相談に行ってみる武田塾尾張旭校の
講師紹介
-
 山本崇太(高卒認定→名市大/薬)
山本崇太(高卒認定→名市大/薬) -
 北村先生(明和高校→ 名古屋大学 理系)
北村先生(明和高校→ 名古屋大学 理系) -
 今北遥子(膳所高校→名古屋大/農)
今北遥子(膳所高校→名古屋大/農) -
 渡辺梨緒(津山高校→愛知県立大)
渡辺梨緒(津山高校→愛知県立大) -
 今泉若葉(名古屋西高校→名古屋大)
今泉若葉(名古屋西高校→名古屋大) -
 大神先生(旭野高校→ 南山大学)
大神先生(旭野高校→ 南山大学)
武田塾尾張旭校の
無料受験相談へ
行ってみよう!
武田塾の「無料受験相談」は、これまで多くの受験生の悩みを解決し、大学受験のサポートをしてきました。
話を聞いて、一番どうしたいかを決めたら、その方法を尊重し、応援します。
独学で頑張っても良いですし、武田塾への入塾も歓迎です。
受験相談のメリット
-

1週間で英単語を1000個覚える方法を教えます
聞いてみて1人でできそうなら入塾しなくても構いません。実際にこれだけで合格している生徒は大勢います。
-

参考書を完璧にする方法を教えます
これが身につくかどうかで合否が決まる、家に帰ってからの勉強法を全て教えます。独学でできる!という方はこの方法とカリキュラムや武田塾のHP、ブログを参考にしながらやってみてください。
-

細かい悩みまで聞きます
『定期テストはどうしたらいい?』『現代文がどうしても伸びない!』などなど何でも聞いてください。すべて明確に答えます。
あなたに合った勉強法を教えます!
無料受験相談に行ってみるあなたに合った勉強法を教えます!
無料受験相談に行ってみる武田塾 尾張旭校
へのアクセス
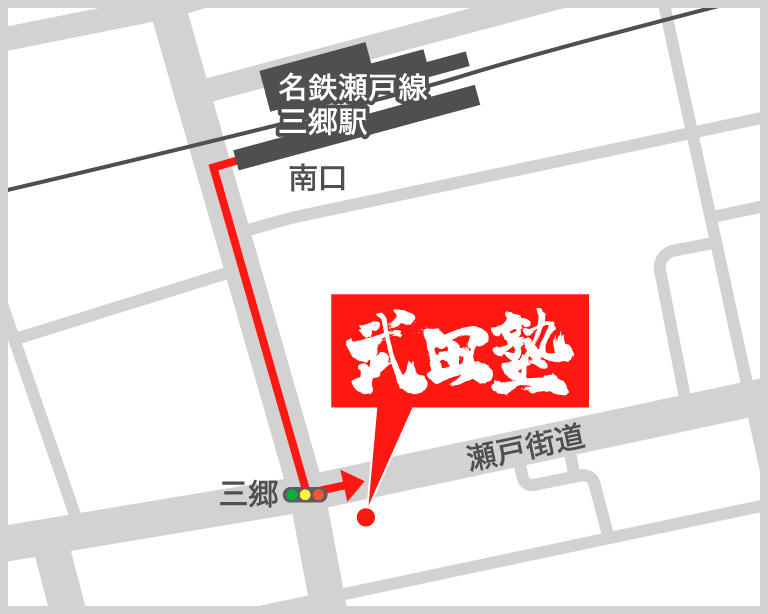
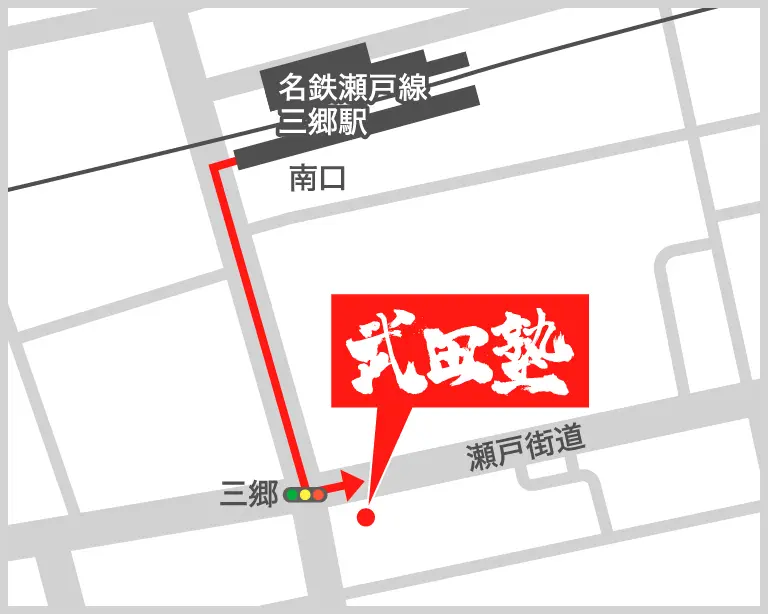
<名鉄瀬戸線 三郷駅南口からの場合>
①名鉄瀬戸線 三郷駅南口から出て左へ進みます。
②道なりに進み、三郷交差点にある井上ビル2階が武田塾尾張旭校です。



















