物理の見直しの仕方について ! 東工大現役合格講師が語ります！

武蔵溝ノ口駅・溝の口駅より徒歩3分

大学受験予備校・個別指導塾の「武田塾　溝ノ口校」です。

今回は、溝ノ口校の講師によるブログです。

内容は「物理の見直しの仕方について」です。

だいぶ難しい内容ですが物理選択の人はぜひ見てください！

それではどうぞ！

物理の見直しの仕方について

こんにちは。武田塾溝ノ口校講師の窪田です。

今回は物理の見直しの仕方についてお話します。

見直し方は2つ！

➀単位に注目する

②極限を考える

です。

それではそれぞれについてお話ししていきます。

物理の見直しの仕方

➀単位に注目する

物理の問題は、難関私大や国公立を除けばほとんどが選択問題です。

そのため、選択肢の単位を見ることで明らかにおかしい選択肢を排除することができます。

例として、2018年度センター物理第2問Aの問2を見てみましょう。

スイッチをa側に入れてから(中略)抵抗で発生するジュール熱を表す式として正しいものを、次の①～➇のうちから一つ選べ。

➀V/R ②V/2R ③V^2/R ④V^2/2R ⑤CV ⑥CV/2 ⑦C➇C/2

さて、見ての通り8つの選択肢の中で同じ単位のものは2個ずつあります。１つずつ確かめていきましょう。

➀と➁はV/Rであり、単位は[A](アンペア)です。

答えとなるジュール熱の単位は[J](ジュール)なのでこの選択肢は間違いです。

➂と➃はV^2/Rです。Vは電位であり、定義は「1[c](クーロン)あたりの静電気力による位置エネルギー」なので単位は[V](ボルト)＝[J/c]です。

V/Rは[A]であり、定義は「毎秒１クーロンの電気量が流れるときの電流の強さ」

（本当はクーロンがアンペアによって定義されておりアンペアは別の方法で定義されるが今回は単位の説明なのでこれでいい）

なので、[A]=[c/s]となります。よってv^2/Rは[V]×[A]=[J/c]×[c/s]=[J/c]となり、これは仕事率の単位なので間違いです。

⑤と⑥はCVです。C=Q/VでありQ (電荷)の単位は[c]なので、Cの単位は[F](ファラド)=[c]/[J/c]=[c^2/J]です。

よってCVの単位は(CV＝Qなので当然だが) [c^2/J]×[J/c]=[c]となり、これは電荷の単位なので間違いです。

⑦と➇はCです。これは[c^2/J]×[J/c]^2=[J]となり、これはジュール熱の単位なので、⑦➇どちらかが正解とわかります。

おわかりいただけたでしょうか。

一見８択にも見えるこの問題は実は２択の問題だったのです。

時間がないとき、選択肢だけ見て２択に絞れば計算しなくても運でいくらか取れそうじゃないですか？

見直しをするとき、計算しなくても明らかに間違っているものをすぐ見つけられそうではありませんか？

このようにある式の単位を調べることを「次元解析」と言います。

今までサクっとこの次元解析をやってきましたが、そのやり方をまとめてみましょう。

例えば［ニュートン］の次元を［長さ］［時間］［質量］で表したいと思ったときは、それらをつなぐ公式、すなわち運動方程式を使います。

F＝maにおいて当然両辺の次元は一致しているので、

［力］＝［質量］×［加速度］＝［質量］×［長さ］×［時間］^(-2)

とわかるわけです。

また、例えば［圧力］の次元を知りたいときはその定義である「単位面積当たりに加わる力」というのを思い出せば

［圧力］＝［力］÷［面積］＝［質量］×［長さ］^(-1)×［時間］^(-2)

とわかります。

以上より、

・求めたい量が含まれる公式を考える

・定義から考える

の2点を押さえれば次元解析は簡単にすることが出来ます。

選択問題に限らず記述式のときでも、常に見直しをするときは次元解析をする癖をつけてください。

【参考】

先ほどは「次元」と「単位」を特に区別せずに話しましたが、両者の概念は大きく異なります。

・次元とは

「次元」とは、［長さ］や［時間］など、その量そのもののことを表しており、すべての次元は

長さ［L］
質量［M］
時間［T］
電流［A］
熱力学温度［Θ］
物質量［N］
光度［J］

の7種類の積で表されます。

この7つは国際量体系（ISQ）によって規定されており、特に高校物理では上４つを使ったMKSA単位系（M：メートル　K：キログラム　S：時間　A：アンペア）でほぼすべての次元を表せます。

例えば
［体積］＝［長さ］×［長さ］×［長さ］＝L＾３
［加速度］＝［長さ］÷［時間］÷［時間］=L・T＾(-2)
［力］＝［質量］×［加速度］＝M・L・T＾(-2)　（運動方程式より）
［エネルギー］＝［力］×［長さ］＝M・L＾２・T＾(-2)　（仕事の定義より）

という感じです。

・単位とは

単位とは、それぞれの次元に大きさの「目盛り」をつけたもので、国際単位系によって厳密に定められています。

ISQの７つの基本量の基本単位をSI基本単位といい、以下のように定義されています。

量　（名称）　［記号］　＜定義＞の順で記載

長さ（メートル）［ｍ］

＜真空中で1秒間の299792458 分の1の時間に光が進む行程の長さ。＞

質量（キログラム）［kg］

＜プランク定数を6.62607015×10−34 ジュール秒とすることによって定まる質量。＞

時間（秒）［ｓ］

＜セシウム133原子の基底状態の2つの超微細構造準位（F = 4, M = 0 および F = 3, M = 0）間の遷移に対応する放射の周期の9192631770倍に等しい時間。＞

電流（アンペア）［A］

＜電気素量を1.602176634×10−19 クーロンとすることによって定まる電流。＞

熱力学温度（ケルビン）［K］

＜ボルツマン定数を1.380649×10−23 ジュール毎ケルビンとすることによって定まる温度。＞

物質量（モル）［mol］

＜6.02214076×1023（アボガドロ定数）の要素粒子又は要素粒子の集合体（組成が明確にされたものに限る）で構成された系の物質量。
モルを使うときは、要素粒子 (entités élémentaires) が指定されなければならないが、それは原子、分子、イオン、電子、そのほかの粒子またはこの種の粒子の特定の集合体であってよい。＞

光度（カンデラ）［cd］

＜周波数 540 × 1012ヘルツの単色放射を放出し、所定の方向におけるその放射強度が 1/683ワット毎ステラジアンである光源の、その方向における光度。＞

そして、お気づきかと思いますがこれら７つの基本単位によりすべての単位は表すことができ、それらをSI組立単位と言います。

以下に例を示します。

組立量	名称	記号	他のSI単位による表し方	SI基本単位による表し方
平面角	ラジアン (radian)	rad	1	m/m
周波数	ヘルツ (hertz)	Hz		s⁻¹
力	ニュートン (newton)	N		m·kg·s⁻²
圧力	パスカル (pascal)	Pa	N/m²	m⁻¹·kg·s⁻²
エネルギー・仕事・熱量	ジュール (joule)	J	N·m	m²·kg·s⁻²
仕事率	ワット (watt)	W	J/s	m²·kg·s⁻³
電荷・電気量	クーロン (coulomb)	C		s·A
電位差 (電圧)・起電力	ボルト (volt)	V	W/A	m²·kg·s⁻³·A⁻¹
電気容量	ファラド (farad)	F	C/V	m⁻²·kg⁻¹·s⁴·A²
電気抵抗	オーム (ohm)	Ω	V/A	m²·kg·s⁻³·A⁻²
磁束	ウェーバ (weber)	Wb	V·s	m²·kg·s⁻²·A⁻¹
磁束密度	テスラ (tesla)	T	Wb/m²	kg·s⁻²·A⁻¹
インダクタンス	ヘンリー (henry)	H	Wb/A	m²·kg·s⁻²·A⁻²
セルシウス温度	セルシウス度	℃	K

・結局なんなの？

さて、いろいろと説明してきましたが結局何が言いたいのかというと、次元と単位をごっちゃにしないでほしいということです。

例えば長さの単位にはメートルの他にインチやヤード、尺や寸など様々ありますが、どれも次元は［長さ］であり計り方が違うだけに過ぎないのです。

これは問題を解くときにはあまり気にしなくていいですが、物理を考えるうえでは重要な概念です。

選択問題に限らず記述式のときでも、常に見直しをするときは次元解析をする癖をつけてください。

②極限を考える

簡単な例を見てみましょう。

問１　質量mの球が速度vで壁にぶつかり、反発係数eで跳ね返った。このときの球の速度は？

問２　質量mの小球が速度vで質量M速度０の大球にぶつかった。反発係数をeとするとき、衝突後の２つの球の速度は？

問１の答えは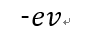

問２の答えは、小球の速度が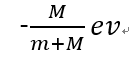大球の速度は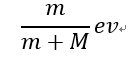です。

さて、物理に限らず問題において問１が問２のヒントになっている場合は多くありますが、

この問１はどうして出題されたのでしょう？

ここで、問２の見直しについて極限を使います。

問２において、大球の質量が∞だとすると、大球は絶対に動かないので壁とみなせます。

つまり、問１と同じ状況になるのです。

よって、問２の答えをM→∞とすると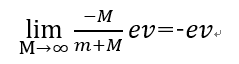、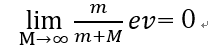となり、問１の答えと一致します。

これにより、極限を考えた上では少なくとも問２の答えは間違っていないということがわかりました。

このように、極限を考えることで時間がない中でも最低限の見直しをすることができます。

自分が出した答えに最低限の整合性があるかどうか、極限を使って確かめえる癖をつけましょう。

以上で今回の僕の話は終わりです。

「もっと詳しく聞きたい」

「物理について議論をしたい」

という人はぜひぜひご連絡ください！

↓↓窪田先生のブログ↓↓

【講師紹介②】東京工業大学に現役合格！東工大の入試傾向について解説します！

【講師ブログ】東工大現役合格生が教える「物理で微積は使うべきか？」

【講師ブログ】東工大現役合格生が教える「オススメの参考書英数物化」

【私立理系】受験科目の勉強時間の配分は？優先すべき科目は？

【教科別】物理の勉強にお困りな人向けに、物理の勉強方法と参考書を紹介します。

【教科別】数Ⅲの授業が終わらないから間に合うか心配。という人！数Ⅲの独学勉強法を紹介します。

【理系】芝浦工大・東京理科大などの私立理系特化型大学の特徴と魅力を紹介します！

■無料受験相談受付中■

志望校の話、文理選択、科目選択、勉強方法などなど

入塾の意思を問わず、どんな悩みや相談にも無料でお応えします！！

「何から始めればいいかわからない」

「勉強の仕方がわからない」

「全然成績が上がらない」

という方は、ぜひ受験相談にお越しください！

◆武田塾の無料受験相談Q&A◆

■武田塾溝ノ口校Twitter■

【公式】武田塾溝ノ口校です！
受験生に役立つツイート・ブログを発信していきます！

ちなみに溝ノ口校では、受験生に役立つブログを350記事以上書いてきました！
ぜひ覗いてみてください！

⇓ブログ記事一覧https://t.co/dO9ujt99Gn
— 武田塾　溝ノ口校 (@tkd_mizonokuchi) September 11, 2020