こんにちは!武田塾小牧校講師のOです。
新年度がはじまりましたね!今年こそ学年1位になる・・・!とか、数学を得意にしたい・・・!や、勉強難しくなるかな、大丈夫かな・・・?といった不安もあると思います。この分野は後でやればいいやって思っていると後で大変な目にあいます。少しずつでも不安な単元は解消していきましょうね。
さて、ブログを書くのは初めてです。何について書こうか迷いましたが、今日は数学についてざっと紹介したいと思います。私は大学で数学を専攻していたのですが、数学にもいろいろな分野があります。大雑把に分けると、①解析学、②代数学、③幾何学、④統計学のように分けられます。これ以外にも離散数学など数理情報的な学問もあります。今回は①解析学と②代数学について、少しWikipediaを参照しつつ見ていきましょう。
①解析学(微分・積分、極限など)

解析学は主に微分積分学です。無限小や極限、収束などの曖昧な部分をもっと厳密化することにより発展していったと言われています。析学の初歩的概念である微分積分学の成立に関する決定的業績は、ニュートンおよびライプニッツらによってもたらされたそうです。ニュートンといわれると皆さんおなじみの運動方程式ですね。
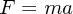
って表せられるものでした。加速度の定義が単位時間あたりの速さということを用いて式を変形することで微分方程式として見ることができます(解くことができます)。物理はどれも(ほぼすべて)このような微分積分学を用いて考えることができます。楽しいですね。
これ以外にも化学平衡も微分方程式が使われているほか、インフルエンザの流行モデル(時間がたつとともに感染者数はどのように変化するか)というSIRモデルも微分方程式を用いて表すことができます。解析学はこのように我々の予想もつかないところで活躍しているんですね・・!楽しいですね。
②代数学(方程式、整数論など)
「代数学」と聞いて皆さんは何を思い浮かべますか???中学校で数学を代数と幾何で分けていたかもしれませんし、問題集が代数編・幾何編って分けられていたかもしれません。予想では代数は「計算」と思われると思います。間違いではないです。
代数学とは数の代わりに文字を用いて方程式の解法を研究する学問として始まりました。文字式の計算(中学校)や式の展開・因数分解(数学Ⅰ)、二項定理や剰余の定理・高次方程式(数学Ⅱ)、ユークリッドの互除法などの整数の性質(数学A)はすべて代数学です。フェルマーの最終定理やがロア理論も代数学です。
私は代数学が専門で、主に整数論(体論)を勉強してきたのですが、とても面白い学問です。今までやってきた簡単な計算や方程式の扱いもすべて代数学あってこそ!っていうのは言い過ぎですが、その部分を定義や導き出しているのは代数学です。ぜひ勉強してみてください。
ということで、今回は解析学と代数学について触れました。この2つの学問だけでも実は世に大きな貢献をしています。数学を勉強する理由がわからない、コンピュータに計算させればいいのではないかとよく言われたりしますが、数学の根本をわかっていないとコンピュータに計算させることもできません。ましてやコンピュータにもできないことはあります。人間はコンピュータと違って”考える”という思考があります。我々がこれから生きていくためにはこの”思考”がとても大事です。思考は簡単にはつくものではないですし、日ごろから考えるということが大事です。少しずつでもがんばっていきましょう。
4月に入りましたがまだまだ夜は肌寒いですね。みなさん風邪には注意してくださいね。
武田塾小牧校では受験勉強などに関するお悩みをいつでも受け付けています。
LINEの友だち追加をして、お気軽に相談してくださいね!
〒485-0029
愛知県小牧市中央2-148 小牧ステーションビル3階301
TEL 0568-44-1086
MAIL komaki@takeda.tv











