こんにちは!武田塾西葛西校講師の横山です!
暖かい季節となってきて勉強しやすい環境となってきました!
新高校3年生の方は受験生という自覚をもって勉強に励んでください!
今回は数学Iの数と式で受験生がミスしがちな問題をピックアップして解説していこうと思います!
①文字係数の1次方程式
問題
(a-2)x+4ay=-1 …①
x-(3a+1)y=a …②
aを実数の定数として、x,yについての連立方程式を解きなさい。
解答
皆さんは解けましたでしょうか?
解けたと思った人も解答を見てみると少し異なっているかもしれません。
まずは、連立1次方程式なので、加減法または代入法を用いてxまたはyについて解きましょう。
今回は代入法を用いて、
②をx=(3a+1)y+a
と変形し、①に代入します。
今回計算分野については言及しないので計算過程を省略すると、
(a-1)(3a+2)y=-(a-1)^2
となります。
ここからが、受験生が間違えやすい箇所なのですが、
数学は0で割ることは許されていません。
つまり、0になる可能性がある文字で割る場合は注意しなければいけません。
(明らかに0よりも大きい場合など(a^2+3)などは考える必要はありません。)
今回で言えば、a=1の場合とa=-2/3の場合は解なしと言いたいところなのですが、
もう一つy以外の部分で両辺が0になる場合も考える必要があります。
(0×y=0といった形です)
この場合はyは解が無数にある状態になります。
結論としては、
a=1の場合、解は無数
a=-2/3の場合、解なし
上記のa以外の実数の場合、x=(4a+1)/(3a+2), y=-(a-1)/(3a+2)
となります。
この場合分けというのは基礎問題精講にもあるのでできなかった人は復習しましょう。
このように融合問題で出されたりするとすぐ忘れる受験生は多いので
文字で割る時や最初から分母に文字がある場合などは計算せずに
まず場合分けがあるかどうか確認をしましょう。
②文字係数の1次不等式
問題
不等式
ax+a>a^2+x …③
を解け。正し、aは定数とする。
解答
今回の問題は先ほどの問題と似ているのでセットで覚えておきましょう。
まず、xについて整理してもらうためにxを左に残りの定数部分を右に移項します。
すると、
(a-1)x>a^2-a
つまり、
(a-1)x>a(a-1) となります。
ここから注意してほしいのですが、先ほどと同様にxについて求める際、
(a-1)という文字で割る必要があります。
これがもし、0であった場合、0・x>0となってしまってxは解なしとなってしまいます。
ここまでは先ほどと同じなのですが、
不等式というのは割るものの符号が正負で不等式の向きが変わるという性質があります。
つまり、場合分けは0の他に、正負でも考える必要があります。
したがって、解答としては、
ⅰ) a-1>0 の場合、③の両辺をa-1で割り、 x>a となる。
ⅱ) a-1=0 の場合、0・x>0となり、解なし
ⅲ) a-1<0の場合、③の両辺をa-1で割り、不等号の向きを逆にすると、 x<a となる。
したがって最終回答は
a>1 のとき、x>a
a=1 のとき、解なし
a<1 のとき、x<a
となる。
どんな時でも、文字で割る時というのは必ず場合分けがないか確かめてから解き始めましょう。
③ルートが入る不等式
問題
√(5-x)<x+1 を解け。
解答
とりあえず、2乗しようとした皆さん、間違いです。
まず、ルートが出てきたらどんな問題でも必ずルートの中身が正かどうかの確認はしておきましょう。
今回の問題はルートの中身が正にならない可能性もあるので、
まず、5-x≧0と書きましょう。
そして、ルート付きの不等号というのは注意してほしいのがルートの値は0以上なので、
必然的に右辺が0以上という範囲を設けなければいけません。
つまり、x+1>0も加えなければなりません。
したがって、xの制約は-1<x≦5となります。
あとはそのまま解くだけなので特にいう事はないと思いますが、
2乗して整理すると、(x+4)(x-1)>0となり、先ほどの範囲と合わせると、
1<x≦5が答えとなります。
解く前に先ほどの2手順を踏まないと答えが間違ってしまう可能性があるので、
ルートが含まれている不等式は範囲絞れないかを確認してから解きましょう。
④次数下げ
問題
x=2-√3 のとき、
x^3-x^2-6x-1…④
を解け。
解答
この問題はミスをしやすいというか一種のテクニックを覚えてほしくて抜粋しました。
代入するだけでしょと思った人、計算しなくてもなんとなく面倒くさそうだなと思いませんでしたか?
その通りです。そのままやると計算が複雑なため、工夫した計算をしましょう。
そこで今回使うのが次数下げです。
次数下げとは何かというと、まず次数というのは文字の右上にある数字のことを言います。
3乗なら3、2乗なら2といったようなものです。これを下げるので
3乗を1乗にするなどを次数下げといいます。
これのメリットは3乗など複雑な計算をせずとも1乗などにしてしまえば、
代入だけで答えが求まるという点にあります。
では、どのようにやるかというと、前提条件から次数が高いものと低いもの両方を持つ式を作ればいいのです。
x=2-√3から、2を左辺に移項して、2乗すると、x^2-4x+4=3という次数が異なるものが出てきました。
これを整理すると、x^2=4x-1となります。
これによって、2乗を1乗と定数に直すことができます。
したがって、次数が下がったことが分かりますね。
(余談なのですが、√3を移項して2乗すると、xの1乗の係数がルートが入って計算がしにくくなるため、2を移項した方が良いです。)
つまり、x^3=x・x^2=x(4x-1)=4x^2-x
4x^2-x=4(4x-1)-x=15x-4
となります。
したがって、④=(15x-4)-(4x-1)-6x-1=5x-4
と1次式にすることができました。あとは代入するだけなので、
5(2-√3)-4=6-5√3
となります。
次数が多い計算などはどうにかして次数を下げることができないか考えて計算してみましょう。
⑤因数分解
問題
2ax^3+(a^2-2ab-2)x^2-(a^2b+a-2b)x+ab
を因数分解せよ。
解答
因数分解する際に、闇雲にやろうとする人がいると思いますが、
それでは、計算が大変な上に、時間がかかってしまうことがあります。
ここで、定石でもある最低次の文字について整理することを意識できるかがカギです。
最低次とは、次数が一番小さいことを言い、今回の問題で言うとbにあたります。
つまり、bについて整理すると、
{-2ax^2-(a^2-2)x-a}b+2ax^3+(a^2-2)x^2-ax
と、bの一次式に整理することができます。
-{2ax^2+(a^2-2)x-a}(b-x)
=-(ax-1)(2x+a)(b-x)
という答えになります。
必ず、因数分解するときは次数に注目してから解き始めましょう。
⑥最後に
今回は、数1,Aの数と式について受験生が間違えやすい問題についてピックアップしました。
受験というのは、応用問題を解けるようにしなくとも、標準問題を完璧に解ければ十分合格点に
足りるようになっています。今回紹介した問題をきっちりできるようになれば、合格へ近づく
と思うので、できていなかった人はもう一度勉強のやり方を見直して励んでください。
武田塾とは
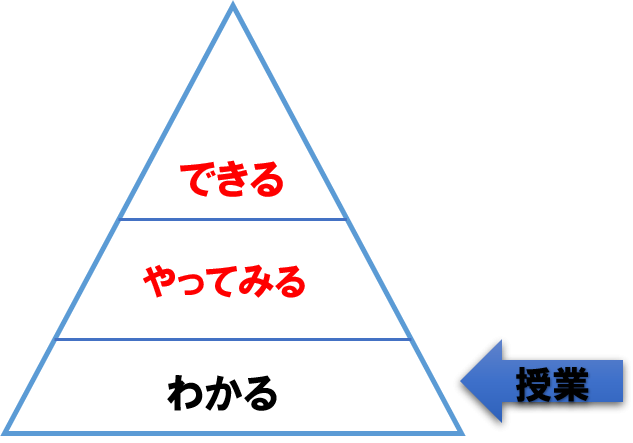
偏差値を上げるためには「わかる・やってみる・できる」の3ステップが必要です
しかし高校や予備校の“授業”では一番下の「わかる」までしかやってくれません。
多くの生徒は授業を受けっぱなしにし「できる」まで到達しません。
勉強は"授業"ではなくその復習である
「やってみる」「できる」の段階こそが重要なのです。
集団授業はムダ!みんなと同じペースでは逆転合格できない。
武田塾の極意:授業をしない!
武田塾の極意:完璧になるまで絶対に先に進まない
自分のレベルに合った参考書を一冊ずつ完璧にする
武田塾では「一冊を完璧に」することを実現するために志望校別カリキュラムを作成し、それに基づいたテストで確実に「わかる」だけでなく「できる」ような仕組みになっています。
志望校別カリキュラムのメリットは…
✓圧倒的に速い!
→ペースが速いうえに繰り返せるという量も質も圧倒的に効率のよい学習方法
✓毎週定期テスト状態!
→その週にやった範囲からランダムでまったく同じ問題を解きなおしてもらいます
✓完璧になるまで徹底的に繰り返す!
→「やりっぱなし・解きっぱなし」をここで根本的に変化させる
武田塾の極意:完璧になるまで絶対先に進まない!
武田塾の極意:基礎の基礎から学び直し、参考書を完璧にする
全部解けるようになるまで何度も繰り返す。
「人は忘れるものである」という前提で勉強する。
忘れた知識を100%に引き戻す作業=復習です ではどのタイミングで復習すればいいのでしょうか?
答えは「忘れる前」です。
武田塾が理想とする復習のタイミングは、まず学習した当日です。そして、週に2日の復習日を設け、その結果をテストで確認します。そこまで徹底して復習しないと勉強は身につきません。

できた問題には「○」
出来なかった問題には「/」をつけ解答と解説を読み
完全に理解しなおすこと。
その際、間違えた理由も書き込んでください。
その日解いた問題をその日のうちに「全問正解」するまで繰り返します。
武田塾の極意:基礎の基礎から学び直し、各段階の参考書を完璧にする!
武田塾の極意:一人ひとり個別に自学自習の「勉強方法」を詳しく教える!そして「サボれない」
2つのチェックでサボれない勉強法を指定します。
①義務自習と365日課題指定
→「何時から何時まで自習にくる」ということを生徒さんと約束し、その時間にしっかり来ているか毎日確認します
そしてその自習時間でどんな勉強をするのかもすべて指定します。
「なにをいつまでにどう勉強すればいいか」一切迷いません。
②帰宅前の宿題チェック
→自習を終えて帰るときには、武田塾のスタッフに1日の勉強内容を報告してから帰ってもらいます。
ペース通りに勉強できているか、勉強法は間違っていないか、悩んでいることはないかなどを毎日確認するため
「このままで大丈夫なのかな」という不安は一切ありません。
毎日のやるべき課題が明確に宿題に出ます。その宿題をもとに自学自習を頑張ってもらいます!
そして特訓の開始時にテストがあるので「できる」ようになることを意識して毎日勉強していたが“ばれる”仕組みになっています。
武田塾の極意:一人ひとり個別に、自学自習の「勉強方法」を詳しく教える!そして「サボれない」ようにする!

武田塾の勉強方法に出会い、偏差値30代から本気で1年間勉強した結果
偏差値を70近くまで伸ばし、青山学院大学の経済学部に現役合格!
そのやり方、特別に教えます!!
大学合格の為の㊙テクニックや、西葛西校でしか聞けないことばかり!
西葛西校(03‐6808‐9856)まで直接お電話ください!
——*…*——*…*——*…*——*…*——*…*——*…*——
武田塾西葛西校
江戸川区西葛西で個別指導塾.予備校探すなら
「日本初!授業をしない。」武田塾
〒134-0088
東京都江戸川区西葛西6-16-7
西葛西駅前三基ビル 502号
TEL:03-6808-9856
開校時間:10:00~22:00
日曜日のみ10:00~19:00まで
最寄り駅:東京メトロ西葛西駅 徒歩2分
無料受験相談受付 西葛西校に無料受験相談
武田塾 西葛西校 - 江戸川区・西葛西駅近く - 予備校いくなら逆転合格の武田塾 (takeda.tv)
——*…*——*…*——*…*——*…*——*…*——*…*——













