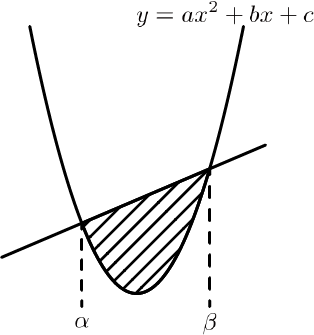
皆さんこんにちは!相模原の大学受験予備校、武田塾橋本校で講師をしています、東京大学のTです。今回から、数学のテクニックを紹介していこうと思います。簡単な問題から難しい問題まで、幅広く応用できるようなトピックを取り扱っていくつもりですので、(更新は遅いと思いますが)ご期待ください!
さて今回は、いわゆる「1/6の公式」というものを中心に、関連する様々な公式や定理、考え方を紹介していこうと思います。中にはマニアックすぎて使えないものや、難しいものもあると思いますが、適当にお付き合いください。
1/6の公式
ある程度数学Ⅱの微分積分を学んだ皆さんは、次のような公式を見たことがあると思います。
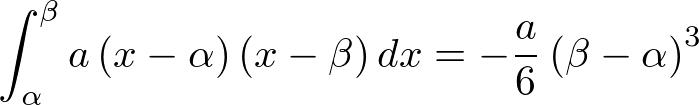
「確かに見たことあるかも」という方、多いのではないでしょうか。「見たことあるけど、何に使うかわからない」という方もいるかもしれませんね。
実はこの式、とっても有能なんです。ですが、式の「見た目」を綺麗にしすぎたあまり、その有能さが見えづらくなってしまっています。
ここで、この式の「図形的な意味」を考えてみましょう。
次の図を見てください。簡単のため、x軸やy軸は省略して描いてあります。
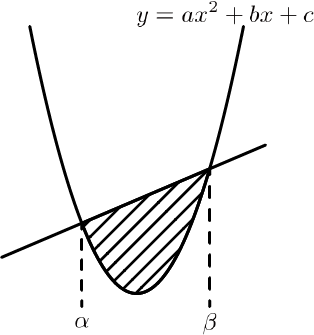
上図の斜線部分の面積S、実はこうなってるんです。
![]()
この形、どこかで見たことありませんか…?
そうです!先ほどの積分の公式の、右辺の形にそっくりなんです!
「二次関数と直線で囲まれた部分」の面積Sは、直線の傾きなどに依存せず、交点のx座標の差と、二次関数の2次の項の係数のみによって決まるんです。有能ですよね。
有能ですよね?
知ってた人はいいんです。
以上が、基本的、基礎的な「1/6の公式」に関する知識です。「なるほど!」と思っていただけたでしょうか?
この1/6の公式ですが、二次関数の性質を知っていれば、様々な部分の面積計算に応用することができます。
1/6の公式の応用〜二次関数の性質
例えば、次の図を見てください。
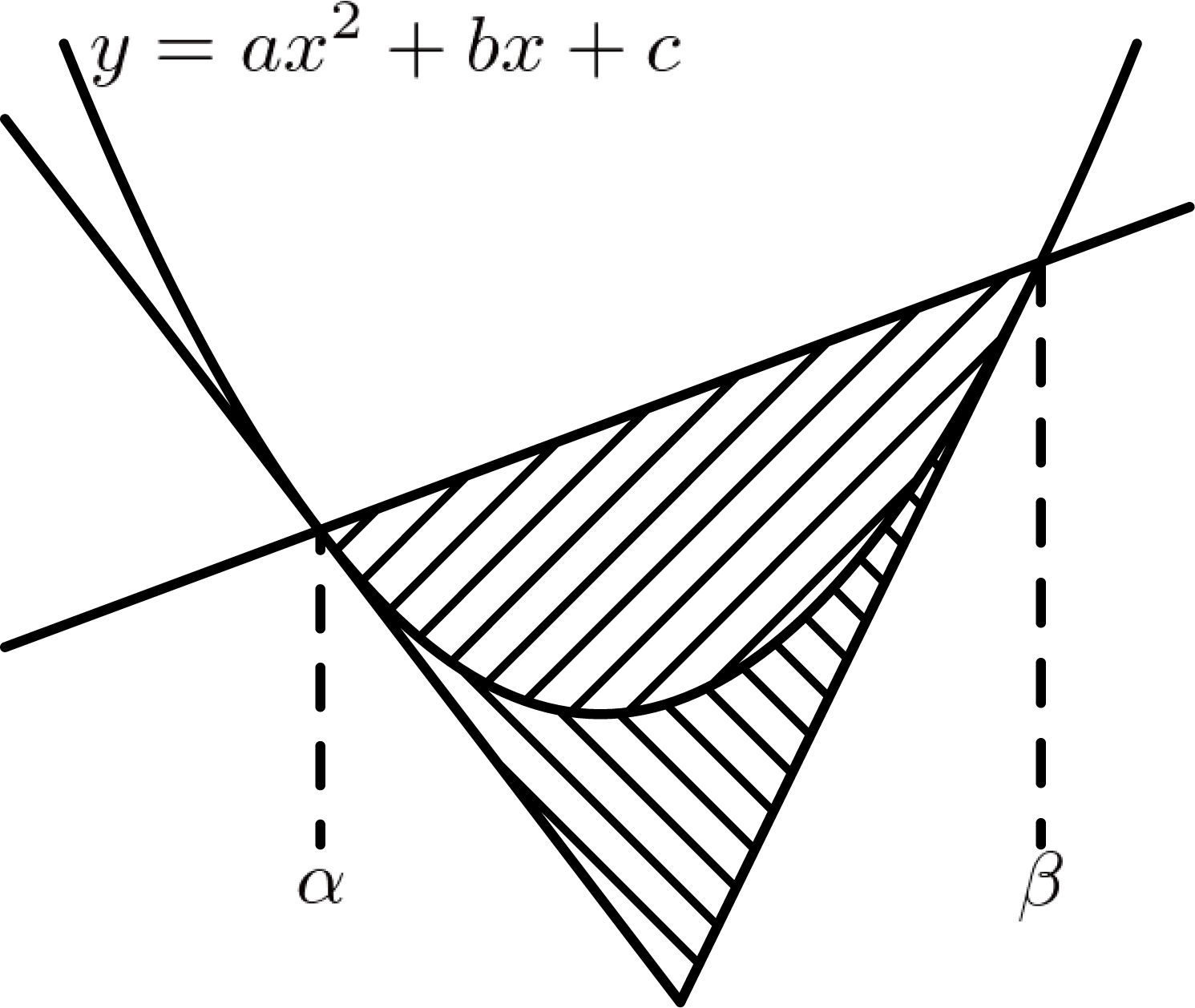
「二次関数とその接線2本で囲まれた部分の面積(\\\の斜線部)と、///の斜線部の面積の比はちょうど1:2になる」という性質があります。ここでは証明は省きますが、文字定数を置いて実際に計算してみるとわかります。この性質はあらゆる二次関数について当てはまります。
先ほどの1/6の公式に当てはめて考えますと、「二次関数とその接線2本で囲まれた部分(\\\の斜線部)」の面積Sはこうなります。
![]()
どうですか?2次の項の係数と、接点のx座標だけわかっていれば、簡単に面積を求めることができるんです。とてもシンプルで綺麗でしょう?
と、少々知識の適用範囲の狭そうなテクニックでしたが、これ以降に紹介するテクニックはこれよりももっと適用範囲が狭いです。
ですが、数学的対象としては、より深く、二次関数のみならず様々な現象を理解する緒になると思いますので、頭の痛くなっていない方はもうしばらく読んでいってください。
1/12の公式
さて、次の図を見てください。これは、「2次の項の係数が等しい二つの二次関数と、その共通接線で囲まれた部分」を表す図です。
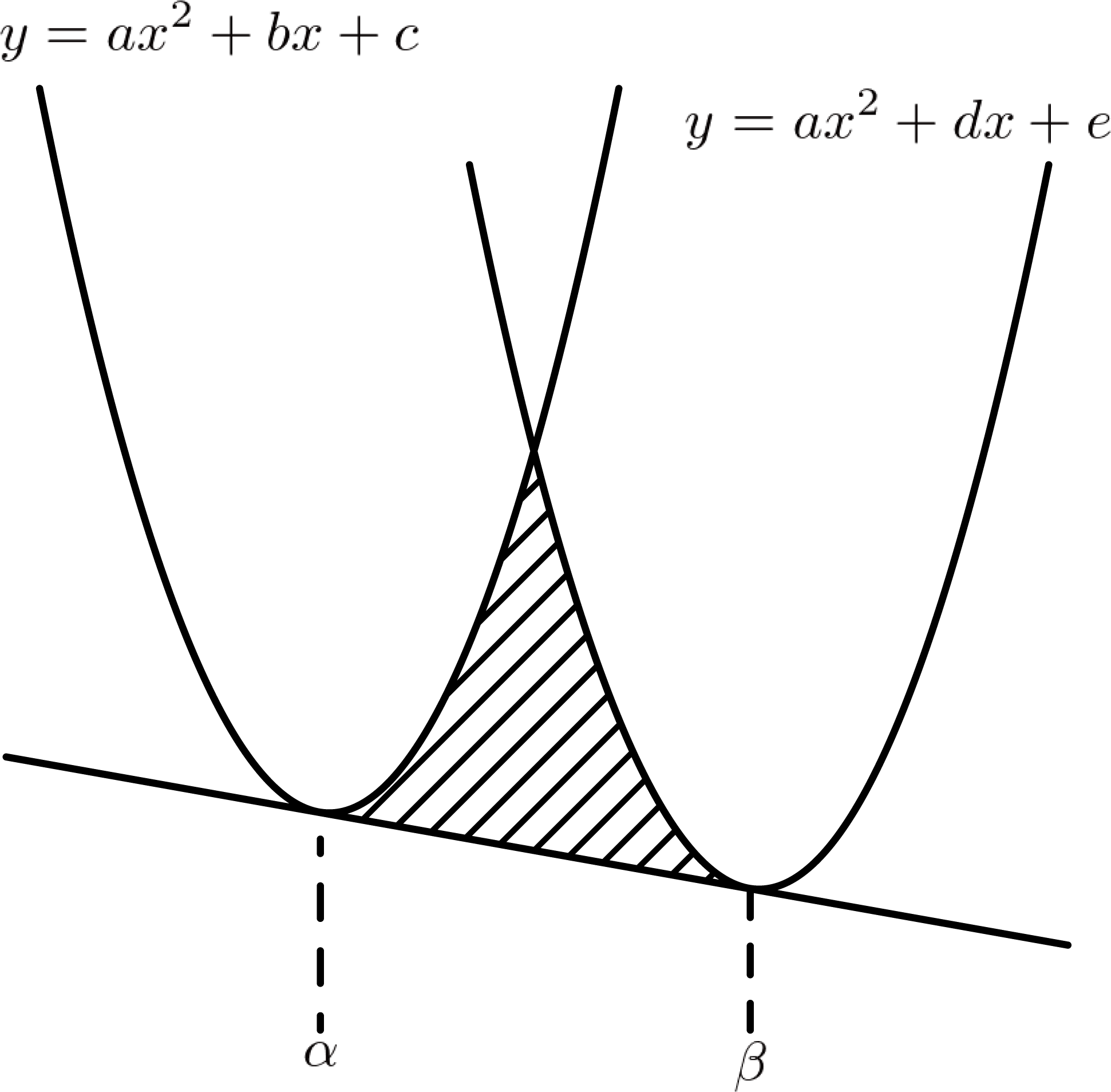
詳しい証明は省きますが、上図の斜線部分の面積Sは次の式で導くことができます。
![]()
またしても、2次の項の係数と、接点のx座標だけわかっていれば簡単に面積を求めることができます。
さて、これはなぜでしょうか?
様々なアプローチの仕方があります。ですが、どの方法も文章化するのが大変ですので、ここでは割愛いたします。紙に鉛筆を走らせて、色々考えてみてください。
橋本校に通っている生徒さんでしたら、直接解説いたします(笑)
今までは数学IIの知識で理解できる範囲(のはず)でしたが、次は数学Ⅲの知識を少々使うトピックですので、未習の方は「ふーん」という感じでどうぞ。
ベータ関数の積分公式、一般化という考え方
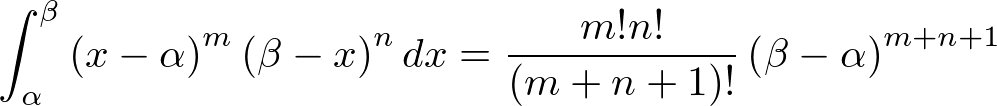
この式がいわゆる「ベータ関数の積分公式」と呼ばれるものです(名称には諸説あります)。
導出の方針を簡単に書いておきます。
こちらの関数を、平行移動やスケーリングをしてやると(式の上では置換積分の操作を行います)、次のような形に帰着することができます。
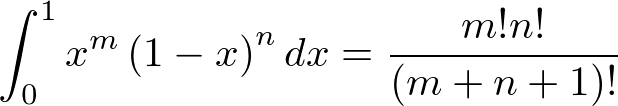
こちらの積分は、部分積分を用いた帰納法によって容易に示すことができます(ここでは略します)。
さて、この「ベータ関数の積分公式」、適応範囲は狭いですが、ハマればものすごく頼もしいんです。この公式を用いることで、「三次関数とその接線で囲まれた部分の面積」や、「四次関数と、それに2点で接する直線とで囲まれた部分の面積」などが、共有点の座標の情報から即座に計算することができます。
冒頭で述べた「1/6の公式」も、m=n=1の場合の「ベータ関数の積分公式」となっています。つまり、この積分公式は「1/6の公式の一般化」であると言えるでしょう。
さて、冒頭の「1/6の公式」、導出せよと言われたら、皆さんはどうするでしょうか?存外単純な等式ですので、どのような参考書にも載っていると思います。当然、地道に計算しても成功すると思います。
数学IIIを勉強した方々にとっては、「平行移動をして簡単にする」「部分積分をする」のふたつにひとつだと思います。
これらふたつの考え方は、1/6の公式の一般化である「ベータ関数の積分公式」の導出の過程で用いられています。
何が述べたいかというと、「証明問題のヒントは、一般化した命題の証明を考えてみると見つかるかもしれないよ」ということです。今回の例は非常に初等的でしたが、「一般化を考えると、考えるべきことが整理されて意外とやりやすい」という事例は、現代数学の中でもままあることです。逆説的で面白いですよね。
面白いですよね?
本当に面白いんでしょうか…。
さて、長くなってしまいましたが、今回のテクニック紹介、いかがでしたか?
最後のセクションなどは特に、コラムの成分が大きかったかもしれませんね。受験生の皆さんの、息抜きになっていれば幸いです。
次回の数学テクニック紹介のテーマは【不等式】です!一流の不等式たちを用意していますので乞うご期待!
ではまた次回、お会いしましょう。
【自立した勉強をするなら】-橋本の予備校 武田塾
武田塾橋本校では、無料受験相談・個別カリキュラム作成・体験特訓を行っております。勉強の仕方、大学受験に向けた参考書の選び方・使い方、モチベーションの上げ方、など受験にまつわるあらゆるご相談に対応させて頂いております。塾生でなくても、無料で行っておりますので、お気軽にご相談くださいませ。ともに学びましょう!
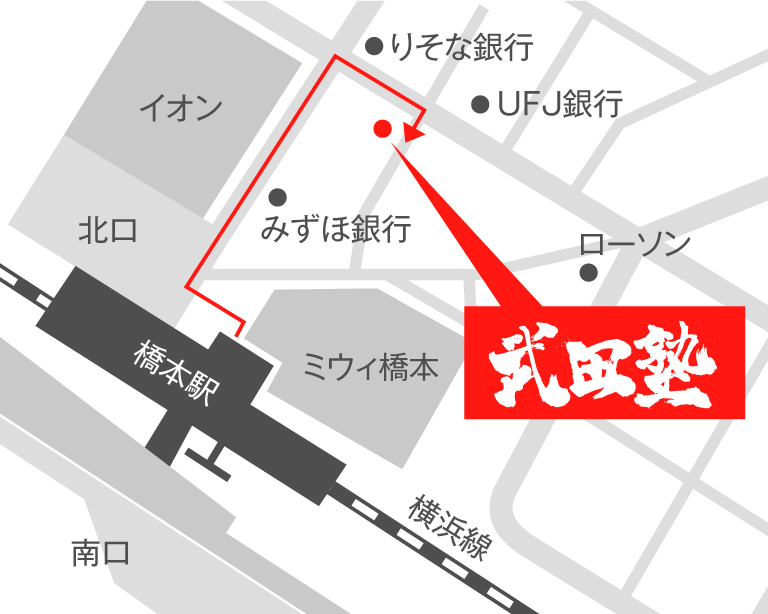 ※橋本駅から徒歩5分!
※橋本駅から徒歩5分!
=============================================
・武田塾ってどんな塾?












