こんにちは！ 武田塾河内松原校です(^^) さて、今回からは定積分の中でも、特殊な解き方をする定積分について書いていきます！ これから数回に分けて書いていくつもりなので、よろしくお願いします(^_^)/ 今回は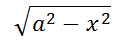 
を含んだ定積分の解き方を紹介します！ この型の問題の解き方は全部で３種類あります。 ① x = asinθと置換する ②円の面積の一部と見て計算する ←オススメ！ ③逆正弦関数を使って解く ではそれぞれの解き方を見ていきましょう！ 
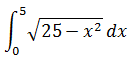を例に考えていきたいと思います。 ①ｘ= asinθと置換する これが最も基本的な解き方です。しかし、他の方法と比べて、計算に時間がかかってしまいます。 実際に計算してみましょう。 x = 5sinθとおくと、 dx = 5cosθdθ [x=0..2] →[θ = 0..π/2] (与式) = ∫[θ=0..π/2]√(25(1-(sinθ)^2)) ×５sinθdθ = ∫[θ=0..π/2]25(cosθ)^2dθ = 25π/4 ②円の面積の一部とみて計算する この方法で計算すると、非常に早く解くことが出来ます。 例を使って考えましょう。 y =√(25 - x^2) を整理すると、x^2 + y^2 = 25 (y > 0) と表せます。 これは原点を中心とした半径5の円を表しています。 積分区間が0→5なので、与式は原点を中心とした半径５の円の面積の４分の１を表していることになります。 よって、 (与式) = 5 × 5 × π × 1/4 = 25π/4 非常に早いですね。この形の問題が出たときは迷わずこの方法で解いてください。 ③逆正弦関数を使って解く この方法は高校ではあまり教えられることがない三角関数の逆関数を用いた公式に当てはめて解く方法です。 知らない人は無視してもらって構いません。 実は逆正弦関数を使ったこんな公式があります。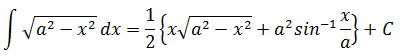 
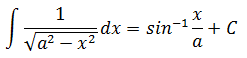これを使えば一気に答えにたどり着くことが出来るわけです。 特に下の方の公式が便利です。 上の方の形になっている場合は②の円の面積とみる方法がオススメです。 計算してみましょう。(なお、表記方法の都合で計算内では逆正弦関数をarcsinと表記します。) (与式) = 1/2[x√(25 - x^2) + 25arcsin(x/5)] (x=0..5) =25/2arcsin1 =25π/4 数式の表記が大変見にくくなっていると思いますがご容赦ください(-_-) 計算過程を結構飛ばして書いているので、もし、計算過程を細かく教えてほしいという方がいましたら、直接聞きに来てください！ 武田塾河内松原校では無料受験相談を実施しております。 また、1週間の無料体験特訓も実施しておりますのでご希望の方は下記リンクからお申し込みをお願いいたします。
